うなり、トレモロについて
2003/3/11
平野拓一(東京工業大学)
1. はじめに
1.1 説明
音の「うなり」(トレモロ, tremolo)について論理的に、数学的に考察する。まず、うなりとは音色の音量がゆっくりと周期的に変化している状態を指す。「音量をふるわせる効果」である(ちなみに、音の高さ=ピッチを震わせる効果はビブラート、vibratoと言われる)。たとえば、オペラなどの歌声で声をのばすときに声を震わせるのもそうであり、バイオリンやフルートの音をのばしたときにゆっくり音が揺れ動いているのもトレモロ(もちろんビブラートの効果も入っている)である。
そして、ほとんど(全て)の生演奏の楽器ではこのようなうなりがあり、コンピュータで規則正しく作り出した音色には無い「ゆらぎ」がある。うなりやその他のゆらぎは人間にとって心地よく感じるようである。その理由は、例えばコンピュータで生のフルートの音の持続音の1周期を切り出し、それをコピーして連続再生してもいい音に聞こえない(しかも、フルートの音とも思えない)ことからも納得できる。
1.2 ゆらぎを再現するためのコンピュータ用音源(PCM音源)
昔のファミコンのPSG(Programmable Sound Generator)音源は無機的で、いかにも人工的な安っぽい音であった。そして少し進化し、MSX2, MSX2+でよく使われていたFM(Frequency Modulation)音源が現れ(今でもパソコンの音源ボードでよく使われるし、最近では携帯電話の音源にも使われている)、かなり音が良くなったものの、依然として生演奏の音にはかなわない無機的なものであった。その理由は音色の波形を演算で作り出しており、規則正しすぎることが原因だった。そこで、コンピュータによる制御で生の楽器の音色に近い音を実現するためにPCM(Pulse Code Modulation)音源(ゲーム機では任天堂のスーパーファミコン、セガのメガドライブあたりから使われ始めた)という音源が現れた。それは、コンピュータで1周期だけ保持して連続再生しても無駄だから、生の楽器の音色をそのまま録音して、必要に応じて少しだけ周波数を変えて再生したりする方式の音源である。生の音を録音するので当然うなりやゆらぎも全てそのまま再現され、いい音が再生される。実際にはピアノの例をだすと、低い鍵盤の音の周波数をそのままコンピュータで処理して高い周波数に直して再生しても高い音の鍵盤を叩いたのと同じ音にはならない。それは物理的にピアノの中で構造が違っている(ハンマーで弦を叩く位置が違う)し、使う弦の種類が違っているから当然である。そこで、PCM音源ではそのような音色の違いにもある程度対応できるようにマルチサンプリングと言っていくつかの異なる高さの音を録音しておいて、再生するときはなるべく近い高さの音の波形を加工して再生するものもある(しかし、これでもまだ切り貼りした音である。例えば、サックスなどで息の微妙な強さの変化に応じた(息を吹き込む音を含む)音を出すことはできない。でも世の中マニアックな人達がいて、さらにこだわって楽器の物理モデルから計算してシミュレーションで音を作り出すものもある。それはYAMAHAのVA音源である)。
ここからは余談である。「MIDI(ミディ)音源」というのはよく聞かれる言葉だが、定義からいうと間違った使い方であり、MIDI音源という音源は存在しない。MIDIとはMusical Instrumental Digital Interfaceの略であり、楽器の演奏情報をケーブルを使って電子的に通信する方式の規格である。日常会話でMIDI音源と言うときはMIDIの通信規格でコンピュータと通信し、コンピュータ(や他のMIDI楽器)から送られてくる信号(MIDIメッセージと言う)にしたがって音を出す音源を指すことが多い。MIDI音源と言った場合にはその音源はPCM音源のものを指すことがほとんどで、内部では送られてきたMIDIメッセージにしたがって録音してあった音を加工して再生しているのである。ただし、最近ではわざわざ音源を買わなくてもパソコンについているオーディオカードでMIDIファイル(拡張子が.midのSMF, Standard Midi File)を再生できることが多いが、そのオーディオカードはFM音源を使っていることが多い。MIDIは演奏情報を通信する規格だから、送られてきた演奏情報どおりに演奏できるならば、その先ではロボットが演奏していてもいいし、人間が演奏していてもかまわない(ただし、人間はそんなに瞬時に反応できないから不可能である)。
2. うなりの数式による説明
2.1 うなりを数式で表す(積でうなりを生成)
1章で述べた音のうなりを式で表してみよう。まず、基本となる音色は簡単のために角周波数![]() の正弦波
の正弦波![]() とする(もちろん一般の音色の波形は数式的に正弦波の和で表すことができるからこのように限定しても一般性を失わない)。その波形の振幅が時間的にゆっくりと大きくなったり小さくなったりする。そのように変化させる波形も簡単のために角周波数
とする(もちろん一般の音色の波形は数式的に正弦波の和で表すことができるからこのように限定しても一般性を失わない)。その波形の振幅が時間的にゆっくりと大きくなったり小さくなったりする。そのように変化させる波形も簡単のために角周波数![]() (周波数が数Hzから数十Hzの小さな値)正弦波
(周波数が数Hzから数十Hzの小さな値)正弦波![]() であるとする。すると、元の波形の振幅の包絡線を
であるとする。すると、元の波形の振幅の包絡線を![]() にするには掛け算すると都合がよく、
にするには掛け算すると都合がよく、![]() にうなりをかけるとき、波形を次のように表してもよさそうである。
にうなりをかけるとき、波形を次のように表してもよさそうである。
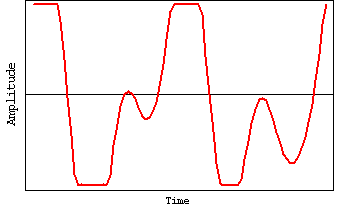
ここで、![]() である。すると、図 1のように基本的には角周波数
である。すると、図 1のように基本的には角周波数![]() の正弦波
の正弦波![]() の音の振幅が時間的にゆっくりと
の音の振幅が時間的にゆっくりと![]() (図中点線の包絡線)で変化していると解釈することができる(無線通信のAM変調と同じ)。
(図中点線の包絡線)で変化していると解釈することができる(無線通信のAM変調と同じ)。![]() ,
, ![]() で、横軸は1秒間を描いたグラフである。
で、横軸は1秒間を描いたグラフである。
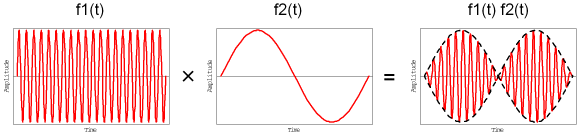
図 1 うなり(トレモロ)
このように三角関数の積に直して、それぞれの周波数が大きく違っていたらうなりであると判断することができる。正弦波の場合には完全に音が消えてしまう時間があり、うなりがかかりすぎるが、実際の楽器の音色だと、多くの高調波(倍音)を含むために全ての倍音でうなり周期が一致するわけではないので完全に音が消えることはまずない。
今のように![]() と掛け算をしてうなりを出すことが可能であるが、1.2節で説明した人工的な音源を使うときなどによく使われる便利なテクニックで、別の方法で式(1)と同じ効果を出すこともできる。その方法について次節で説明する。
と掛け算をしてうなりを出すことが可能であるが、1.2節で説明した人工的な音源を使うときなどによく使われる便利なテクニックで、別の方法で式(1)と同じ効果を出すこともできる。その方法について次節で説明する。
2.2 近い周波数の同じ音色の2音の和でうなりを出す(和でうなりを生成)
2.2.1振幅が等しい正弦波の場合
ここでも簡単のために音色として正弦波を考える。うなりは2つの近い周波数の音が同時に鳴ることによって発生する。なぜそうなるのか数式を使って証明する。今、角周波数![]() の正弦波
の正弦波![]() と角周波数
と角周波数![]() の正弦波
の正弦波![]() を同時に鳴らしたとする。そのとき音は
を同時に鳴らしたとする。そのとき音は![]() となる。式で表すと、
となる。式で表すと、
![]()
![]()
![]()
となる。![]() を三角関数の「和→積公式」で式変形してうなりが現れることを示す。
を三角関数の「和→積公式」で式変形してうなりが現れることを示す。
![]()
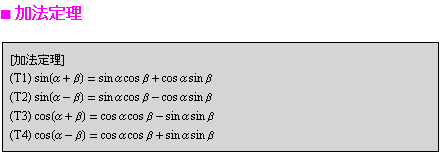


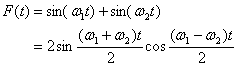
ここで、うなりが発生するためには2つの音の周波数がほとんど同じであることが必要条件である。そこで、
![]()
と![]() は
は![]() に対して
に対して![]() (微少量)だけずらすことにする。
(微少量)だけずらすことにする。
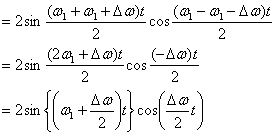
![]() と仮定しているので、
と仮定しているので、![]() の項が音の高さを決め、その振幅の包絡線(音量に対応する)が時間的に角周波数
の項が音の高さを決め、その振幅の包絡線(音量に対応する)が時間的に角周波数![]() でゆっくりと変化していることになる。
でゆっくりと変化していることになる。![]() なので、
なので、![]() の項の角周波数は
の項の角周波数は![]() と近似できる。
と近似できる。
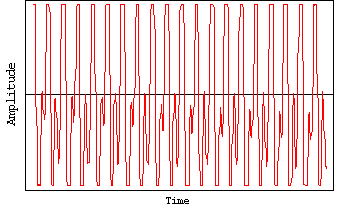
音の波形としては式(2)は2.1節の式(1) と全く同じ性質を持ったものであり、周波数が少し違った2音の和でうなりが発生することがわかる。
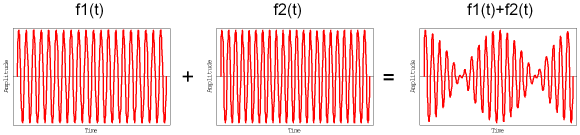
図 2 少し周波数をずらして足すとうなりが発生
図 2は![]() ,
, ![]() で、横軸は1秒間を描いたグラフである。
で、横軸は1秒間を描いたグラフである。
2.2.2 振幅が等しくない正弦波の場合
![]()
この場合はこれ以上式変形できないが、次のように変形して考えるとよい。
![]()
第一項{}内は前節で議論したものであり、うなりを起こす。2項はそれ以外の項であるが、うなりを起こすときは2つの同じ波で周波数が少しずれることが条件である。よって、普通は第2項は0のときの議論をするのだが、![]() と
と![]() の大きさの差が小さいときは第2項のような小さな
の大きさの差が小さいときは第2項のような小さな![]() 成分も残ると考えればよい。
成分も残ると考えればよい。
2.2.3 一般の音色(周期波形)の場合
![]()
複素フーリエ級数で表す
![]()
ただし、![]() であり、
であり、![]() は周期波形の周期、
は周期波形の周期、![]() は基本波の角周波数である。
は基本波の角周波数である。
![]()
![]() は実数だから、
は実数だから、![]() は
は![]() が正負のときで互いに共役となり、
が正負のときで互いに共役となり、![]() もそうであるから、共役複素数同士の積もまた共役複素数となり、絶対値が同じで符号が違う
もそうであるから、共役複素数同士の積もまた共役複素数となり、絶対値が同じで符号が違う![]() のときのシグマの中の値を足すと実部の2倍(実数)となる。いま、
のときのシグマの中の値を足すと実部の2倍(実数)となる。いま、![]() のときの成分だけを抜き出して考えると、
のときの成分だけを抜き出して考えると、
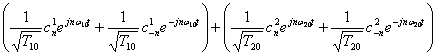
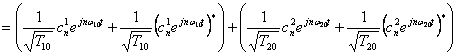
![]()
簡単のため、振幅は等しいとする(等しくない場合も2.2.2節の議論で簡単に式変形できる)。
![]()
![]()
![]()
ここで、
![]() は
は![]() に比べて少しだけ周波数をずらしているのだから
に比べて少しだけ周波数をずらしているのだから![]() と表現できる。すると、フーリエ変化の伸縮律
と表現できる。すると、フーリエ変化の伸縮律![]() より(フーリエ級数はフーリエ変換の特殊な場合と考えることができるので、フーリエ変換の公式が使える)、
より(フーリエ級数はフーリエ変換の特殊な場合と考えることができるので、フーリエ変換の公式が使える)、
![]()
ここで再び簡単のために振幅が等しくなるような係数だったとしてみよう(再び言うが、2.2.2節の議論を見れば振幅が等しくないときの議論も簡単)。
![]()
![]()
![]() なので、
なので、![]() は音の高さを決める基本の波の角周波数、
は音の高さを決める基本の波の角周波数、![]() はうなり角周波数となる。このように各倍音(異なる
はうなり角周波数となる。このように各倍音(異なる![]() )でうなり角周波数が違うので楽器の音色だと完全に音が消える瞬間はなくなる確率が高い。
)でうなり角周波数が違うので楽器の音色だと完全に音が消える瞬間はなくなる確率が高い。
3. 「うなり=トレモロ」の身近な現象と応用例、いい音色とは?
例えば、同じ周波数の音を出す2つの音叉を用意し、片方の音叉だけに粘土などで少し重りを付けて周波数を少しずらし、2つの音叉を同時に鳴らすとはっきりとしたうなりが現れる。一見不思議な現象に思えるが、2.2節で説明したように高校で習う三角関数の公式さえ知っていれば簡単にわかる現象である。
もう一つの例としてホールの残響音による音の響きを考えてみる。周りに音を反射するものが何も無い荒野で音楽を演奏してもいい音には聞こえない。コンサートホールのような場所は音をある程度反射させて残響音(エコー, echo)を残しているのである。この現象はスピーカーの音にも当てはまる。スピーカーの箱は普通巨大なものだが、あの箱の中身はほとんど空っぽである。だからと言って箱無しでは全然いい音が出ず、聴き比べてみると単なる箱なのにすごく重要な役割をしていることがわかる。スピーカーの箱は音を共振させる働きがある。他の同じ現象としては狭くて音をよく反射して残響音が残る風呂で歌ったり、カラオケでエコーをかけると歌がうまくなったように聞こえる現象がある。しかし、音が良くなったように感じるのは共振やエコーだけの効果ではない。楽器の波形を見てもわかるように、フルートやバイオリンの持続音を出したときは音量だけでなく、周波数も多少ゆらいでいる。このゆらぎがいい音に感じるという理由は1.1節で説明したが、2.2節の説明のように、周波数もゆらいでいるビブラートがかかった2つの音が和として足し合わさるとさらにトレモロ効果が起こる。よって、残響音が全くないときよりもさらにうなり=トレモロによって音に潤いが出て、いい音になったと感じるのではないだろうか。
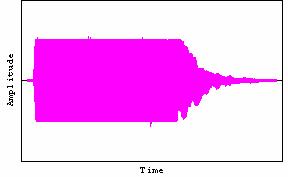
(a) フルートの音色の波形 (Roland SC-88VL)
(b) フルートの音色の1周期の波形。(a)の横軸左から1/4辺り
(c) フルートの音色の10周期の波形
(d) フルートの音色の30周期の波形
図 3 フルートの音色の波形
図 3にフルートの音色の波形を示す。(c)を見ると(b)の一周期波形からかすかにしかゆらいでいないが、このかすかなゆらぎがいい音として現れる。
もう一つFM音源におけるうなりの実用的な応用例を説明する。FM音源ではいろいろな楽器の音が出るがどうもピアノなどの単音を鳴らしてもいい音という感じがしない。それは1.2節で説明したように波形が規則正しすぎるからである。そこで、2.2節で説明した方法で音色に少しうなりを与えると不思議なことにかなりいい音になったように感じるのである。その方法は同じ楽器で同じメロディーを演奏する2つのパートを容易し、片方のパートの音の周波数をほんの少しだけずらすのである(パート1が440Hzを基準にするとしたらパート2は442Hzを基準にするという程度の差)。これは私が中学の頃、MSX・FANという雑誌のFM音楽館というコーナーの説明を読んで、MSXのFM音源プログラムでよく使っていたテクニックである。このトレモロ効果(Roland SC-88VL 取扱説明書 p. 80には「セレステ効果」と書かれている)で音に潤いを与えるテクニックは昔コンピュータやゲーム機でFM音源が主流だった頃活躍していた。FM音源(YAMAHAが開発)は波形を発生させるオペレータと周波数変調するモジュレータで構成されているのだが、FM音源のチップ(OPLLなど)にはオペレータが出す周波数をわずかに変化させるディチューンと言う機能がある。これの機能を使うと2パートも使わないでトレモロ効果を出せる。わざわざ2パート使ってトレモロ効果を出す方法は擬似ディチューンと呼ばれていた。FM音源の場合には音が貧弱だったためこのようなテクニックが使われたが、内部にPCM音源を持っているMIDI音源はそのような小細工をする必要はない。あえて音に厚みを付けたいときでも、より高度なエフェクタ機能があるのでそれを用いる。
さて、ではコンピュータの演算だけで生の楽器の音に劣らない音色を作り出すことは不可能なのだろうか?最初から「自然にはかなわない」と言ってしまうのは論理的ではない。せっかくここまで音色の奥行きと潤いについて考察したので考えてみると、VA音源の物理モデルのようにシミュレーションで音を作り出し、その音にカオス、フラクタル理論などを用いて適当にゆらぎを与えてやればできるのではないだろうか(実はマクロな視点から見たゆらぎの性質はわかっており、「1/fゆらぎ」、「エフ分の1ゆらぎ」と呼ばれる。その発生原因についてはまだ解明されていないようだが、心臓の鼓動周期、ろうそくの明るさの変化など自然界のいろいろなところで見られる現象のようである)。多くの演算を必要とするが生の楽器に劣らない(勝りもしないけど)音色をコンピュータの演算だけで作り出すことは可能であるように思える。